Task: Street Race

Figure 1 gives an example of a course for a street race. You see some points,
labeled from 0 to N (here N=9), and some arrows connecting them.
Point 0 is the start of the race; point N is the finish. The arrows
represent one-way streets. The participants of the race move from point to point
via the streets, in the direction of the arrows only. At each point, a
participant may choose any outgoing arrow.

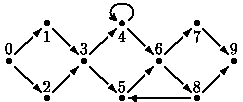
Figure 1: A street course with 10
points

A well-formed course has the following properties:

1. Every point in the course can be reached from the start.
   
2. The finish can be reached from each point in the course.
   
3. The finish has no outgoing arrows.

A participant does not have to
visit every point of the course to reach the finish. Some points, however, are
unavoidable. In the example, these are points 0, 3, 6, and 9. Given a
well-formed course, your program has to determine the set of unavoidable points
that all participants have to visit, excluding start and finish (Subtask A).

Suppose the race has to be held on two consecutive days. For that purpose the
course has to be split into two courses, one for each day. On the first day, the
start is at point 0, and the finish at some `splitting point'. On the second
day, the start is at this splitting point and the finish is at point N.
Given a well-formed course, your program has to determine the set of splitting
points (Subtask B). A point S is a splitting point for the well-formed
course C if S differs from the start and the finish of C,
and the course can be split into two well-formed courses that have no common
arrows and that have S as only common point. In the example, only point 3
is a splitting point.

Input Data

The file INPUT.TXT describes a well-formed course
with at most 50 points and at most 100 arrows. There are N+1 lines in the
file. The first N lines contain the endpoints of the arrows that leave from the
points 0 through N-1 respectively. Each of these lines ends with the
number -2. The last line contains the number -1.

Output Data

Your program should write two lines to the file
OUTPUT.TXT. The first line should contain the number of unavoidable
points in the input course, followed by the labels of these points, in any order
(Subtask A). The second line should contain the number of splitting points of
the input course, followed by the labels of all these points, in any order
(Subtask B).

Example Input and Output

Figure 2 gives possible input and output files
for the example of Figure 1.

_____________     ______________
| INPUT.TXT |     | OUTPUT.TXT |
|___________|     |____________|
| 1 2 -2    |     | 2 3 6      |
| 3 -2      |     | 1 3        |
| 3 -2      |     |____________|
| 5 4 -2    |                   
| 6 4 -2    |                   
| 6 -2      |                   
| 7 8 -2    |                   
| 9 -2      |                   
| 5 9 -2    |                   
| -1        |                   
|___________|                   

Figure 2: Example input and output

---